Materiały » Zadania interaktywne 



ZADANIA INTERAKTYWNE
Projekt "E-laboratorium matematyczne - małymi krokami do wielkich sukcesów"
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.


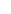

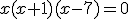
 do
do 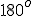
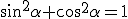 , oraz
, oraz